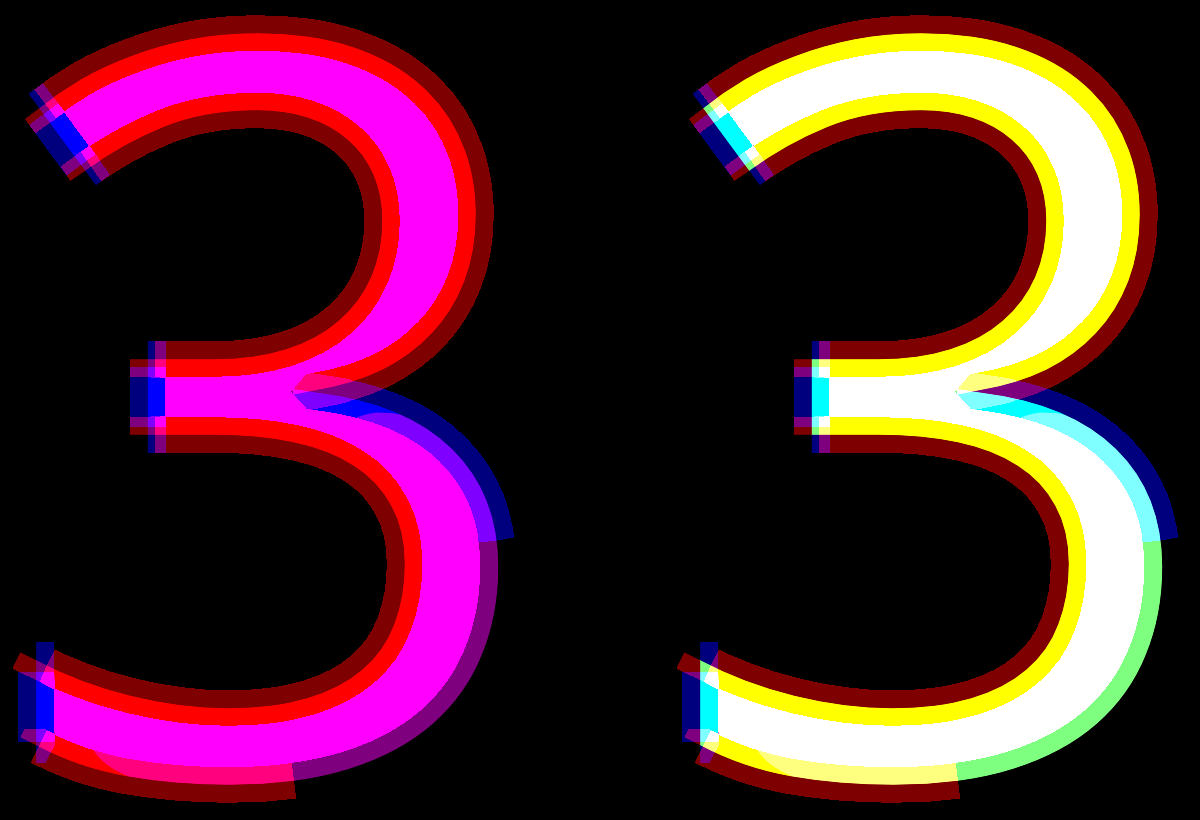cgTalk #04
Fun with distance fields
Are we there yet?
A note on navigation
- space for the next slide
- backspace for the previous slide
- left/right to jump to the next chapter
- up/down to navigate in current chapter
Why?
Agenda
- Distances
- 2D-Distance maps
- 2D-Distance functions
- 3D-Distance fields - functions
- 3D-Distance fields - geometries
Distance
Distance
What's distance?
- the property created by space between two points
- What's space? $~\rightarrow~\mathbb{R}^n \rightarrow \mathbb{R}^2, \mathbb{R}^3$
Distance functions dist(p, q)
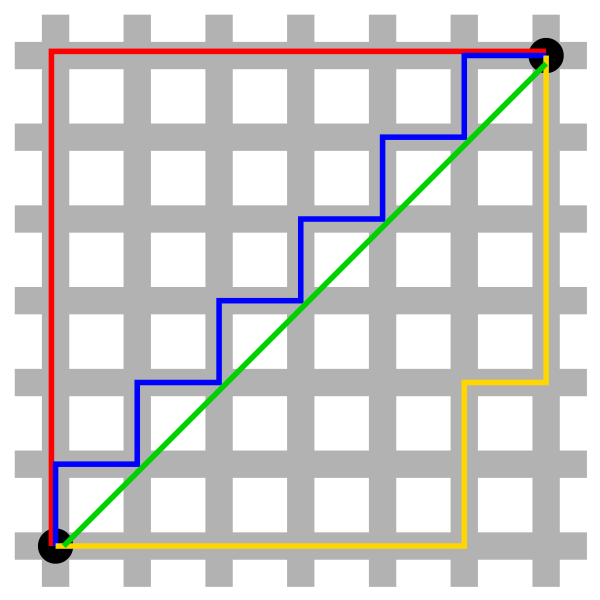
- euclidean distance:$~\textbf{dist}(p, q) = \sqrt{\sum_{i=0}^{n}{(p_i - q_i)^2}}$
- manhattan distance:$~\textbf{dist}(p, q) = \sum_{i=0}^{n}{\lvert p_i - q_i\rvert}$
Distance fields
Distances (distance field values) can be obtained by
- sampling distance field maps
- greyscale, rgba-encoded, ...
- great for complex patterns (glyphs, ...)
- evaluating distance functions
- euclidean, manhattan, ...
- no sampling!
- only trivial "objects"



Using distances
Input
- 2D: texture Coordinate, 2D-coordinate on surface, ...
- 3D: generated 3D (camera)-ray, ...
Output:
- boolean: use
mixto blend the "in"-color:colRes = mix(colIn, colRes, step(0.0, distance)); - anti-aliasing fade:
- use
fwidthto calculate fade-width - blend between 0-1 using
smoothstep
colRes = mix(colIn, colRes, smoothstep(0.0, fwidth(distance), distance)); - use
- bonus: widen the falloff for a glow
colRes = mix(colIn, colRes, smoothstep(0.0, glowDistance, distance));
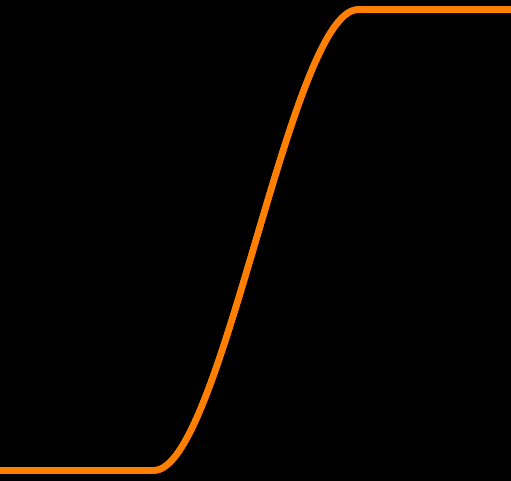
smoothstep
2D-Distance maps
SDF-Textures
SDF - Signed Distance Field
-
encode distance to the other side using signs
- 0, distance to 1: $ \rightarrow <0$
- 1, distance to 0: $ \rightarrow >0$
- shift distance into "single-channel" range:
- $<0 \rightarrow [0; 0.5)$
- $>0 \rightarrow (0.5; 1.0]$

original

sdf
Using SDF 1/3
- load small sdf-map with bilinear filter!
- sample distance field texture
- use 0.5 as an edge between color A and color B
- throw a
fwidthin themix
uniform sampler2D u_SdfMap;
varying vec4 v_Color;
varying vec2 v_TexCoord;
void main() {
float distance = texture2D(u_SdfMap, v_TexCoord).a;
float width = fwidth(distance);
float alpha = smoothstep(0.5 - width, 0.5 + width, distance) * v_Color.a;
gl_FragColor = vec4(v_Color.rgb, alpha);
}

nearest | bilinear
Using SDF 2/3
- small sdf-map allows for large rendering
- fast: single HW-based filtered value + minimal computation
- dynamic thickness: change the edge-value

320x320
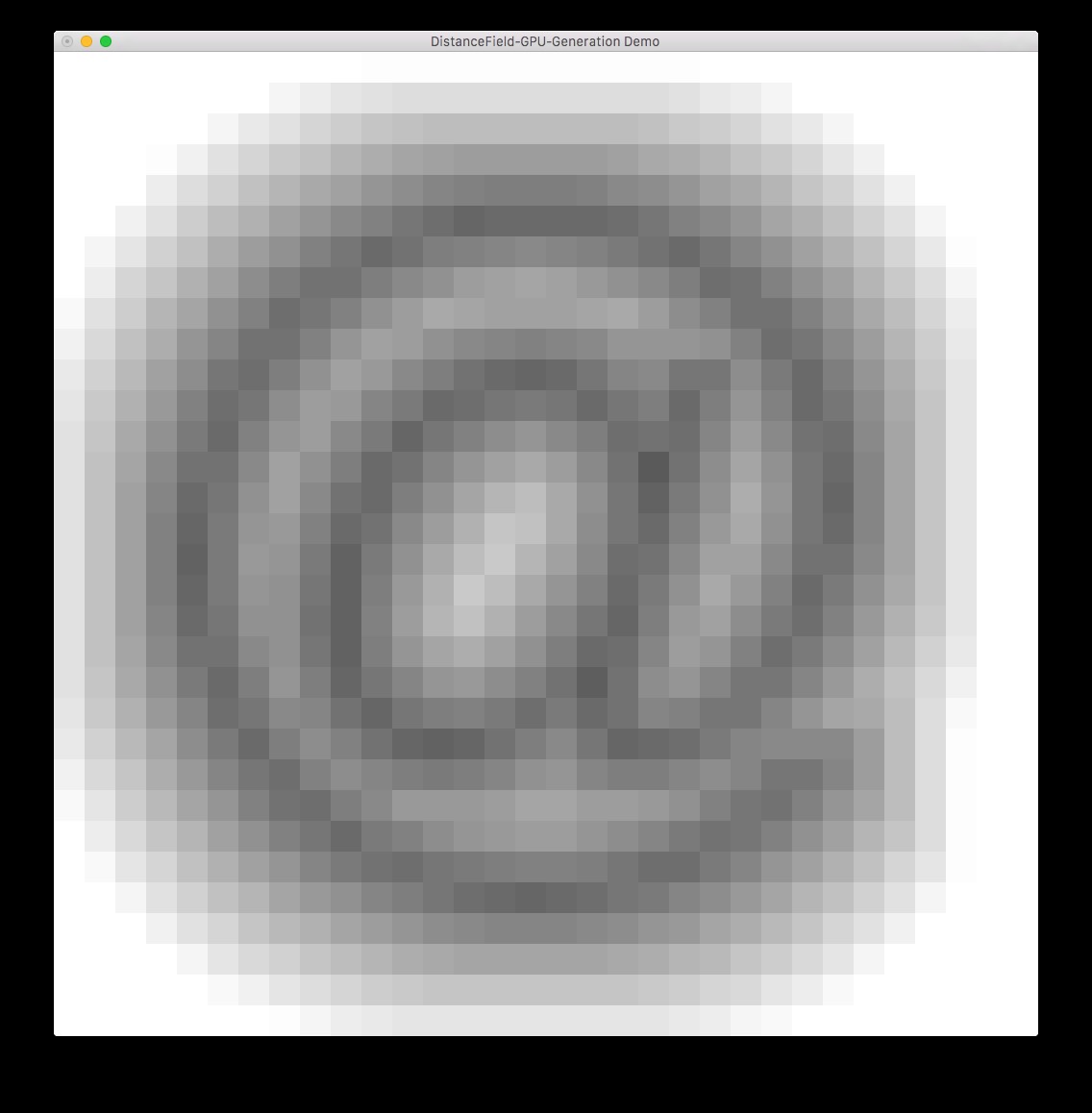
sdf:32x32
Using SDF 3/3
Problems with SDF's
- fine structures are lost in SDF sampling
- bilinear interpolation can be recognized (see here)
- multiple bit-planes not always combinable (see here)



Generating a SDF
Basic idea:
- Input:
- large texture (e.g. $4096^2$)
- target output size (e.g. $64^2$)
- spread for effect (e.g. $32$)
- Calculate distance field for target texture:
- for every texel calc corresponding in/out value
- calculate distance to nearest "other" texel
- map distance into target-range
Note: there are more efficient algorithms out there.
Generating a SDF on the GPU 1/2
Now let's use some shaders for that :-)
- use ping-pong Render-To-Texture: A $\rightarrow$ B $\rightarrow$ A
- Filter original-sized images with simple GLSL Image-Filters:
- Store marked bit & target vector to other side
- Detect edges in source image: mark it, target=(0/0)
- Iterative PP-RTT until whole texture marked:
- For every pixel of current texture
- if (not marked) & any(neighbour $n$ marked):
- mark current
- target = min($n$.target + ($n$ - current))
- if (not marked) & any(neighbour $n$ marked):
- For every pixel of current texture
- Convert target vector to distance (max distance = $s\sqrt{2}$)
- Render texture into final texture for target resolution
Generating a SDF on the GPU 2/2

input image

init

step 16

step 4

step 32

output image
2D-Distance functions
2D-Distance functions
Alternative to distance maps: evaluate a distance function!
- For certain primitives a function is easy:
circle(pos, center, rad) = length(pos - center) - rad; diamond(pos, center, rad) = dot(abs(pos - center), vec2(1.0)) - rad; - Even complex shapes can be realized: Antialiased 2D Grid, Marker, and Arrow Shaders
- works great with fragment derivative antialiasing!
- functions can be combined (think CSG!) and repeated
union(dist1, dist2) = min(dist1, dist2); subtract(dist1, dist2) = max(-dist1, dist2); intersect(dist1 = dist2) = max(dist1, dist2); - the coordinate system can be transformed
Simple 2D-Distance functions 1/2
circle(pos, center, rad) = sqrt(pow(pos - center, 2.0)) - rad;
diamond(pos, center, rad) = dot(abs(pos - center), vec2(1.0)) - rad;Simple 2D-Distance functions 2/2
union(dist1, dist2) = min(dist1, dist2);
subtract(dist1, dist2) = max(-dist1, dist2);
intersect(dist1 = dist2) = max(dist1, dist2);
rotate(coord) = mat2(cos(ang), -sin(ang), sin(ang), cos(ang)) * coord;2D Metaballs
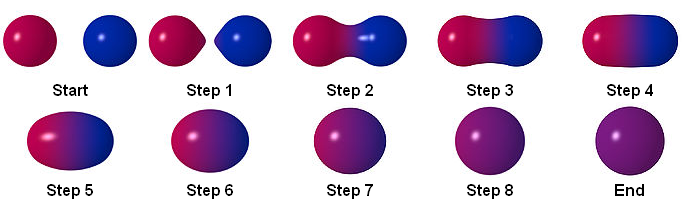
- Metaballs are organic looking objects, that can "stick" together.
- Each ball is defined through a distance function $f$: $$f(x, y, z) = \frac{1}{(x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2}$$
- The distance of multiple metaballs is added together: $$balls(x, y, z) = \sum_{i=0}^{n}f_i(x, y, z)$$
- If the summed distance is bigger than a threshold, the metaball is depicted solid.
Animating multiple 2D Metaballs
shadertoy (the23)
Animating 2D-Distance functions
Let's see what we can do with the following setup:
- distance functions: circle + x-axis-parallel rectangle
- screen segmented into 2d-grid of cells
- use time for animation



Animating 2D-Distance functions
Complex example: 2D-Distance functions
Slightly different scenario:
- Keep the circle.
- Add a distance function for a heart. (tad complicated, see Antialiased 2D Grid, Marker, and Arrow Shaders....)
- Add a distance function for a quad:
vec3 drawQuad(vec3 col, vec2 coord, vec2 p1, vec2 p2, vec2 p3, vec2 p4, float thickness, vec3 oldColor) { float sideA = sign(cross2D(coord - p1, p2 - p1)); float sideB = sign(cross2D(coord - p2, p3 - p2)); float sideC = sign(cross2D(coord - p3, p4 - p3)); float sideD = sign(cross2D(coord - p4, p1 - p4)); float dst = abs(sideA - sideB) + abs(sideB - sideC) + abs(sideC - sideD) + abs(sideD - sideA); dst = clamp(dst, 0.0, 1.0); vec3 res = mix(col, oldColor, dst); res = drawLine(col, coord, p1, p2, thickness, res); res = drawLine(col, coord, p2, p3, thickness, res); res = drawLine(col, coord, p3, p4, thickness, res); res = drawLine(col, coord, p4, p1, thickness, res); return res; }
Complex example: 2D-Distance functions
3D-Distance fields
Raymarching - Functions
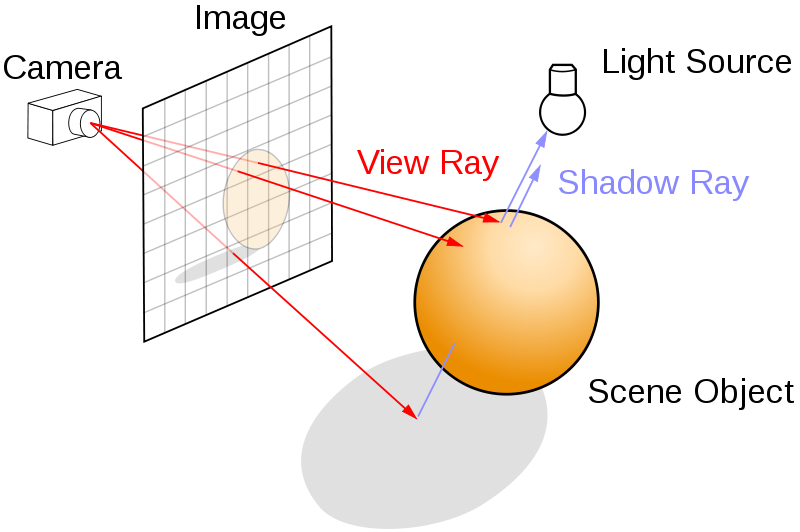
(Recap) Raytracing
Raytracing is a rendering method
- Rays (from the camera) are traced through the scene:
- A view (or secondary, ...) ray is intersected with the scene
- Result is an exact, "singular" hit with "noise" artefacts
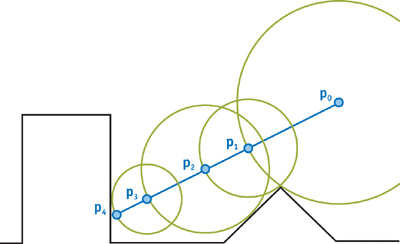
Raymarching
Raymarching is related to raytracing
- Rays from the camera are marched through the scene:
- At every step distances to all scene objects are evaluated
- The smallest distances leads to a new startpoint
- The march terminates if either
distance $<$ threshold || z-Limit || step limit
Raymarching
Implementation in a fragment shader:
r = generateRayForProjection(texCoord, fov);
while !(step-limit || z-limit)
d = getClosestDistanceWithScene
if (hitpoint < threshold)
break; CommenceShading
r.origin += r.dir * d;
if CommenceShading
Potentially repeat above (shadow, reflection, AO, ...)Raymarching - Distance Functions
Great overview of distance functions here
 |
 |
 |
 |
 |
 |
- Distort/transform the input position for a model
- repeat the primitive position
- CSG
(a, b):- union:
min(a, b) - subtract:
max(-a, b) - intersect:
max(a, b)
- union:



Raymarching - Scene
Here's a full, complex example on what can be done:Raymarching - Illumination
Shading needs a normal: evaluate the scene around the hitpoint to obtain new "hitpoints" that form the normal.
Shadows
- The amount of light that shines onto a surface determines if it's in shadow.
- This is determined by the visibility of the lights from a surfacepoint.
- Trace again: from light towards hitpoint:
- if you hit something else, hitpoint must be in shadow.
- Bonus: soft shadows (penumbra) are cheap :-)

Raymarching - AO & reflection
Marching the scene from the hitpoint along the normal can be usefull for other Illumination effects:
- AmbientOcclusion is calculated by marching the scene around the normal
- Reflections can be calculated by marching the scene along the normal
3D-Distance fields*
Raymarching - Geometries
*ok, it's not really distances, but still fun and related ... somewhat
Raymarching - Geometries
In most real life applications we don't have many distance functions:
- we have polygonal geometries,
- where it's pretty darn hard to come up with distance functions!
In order to still use the benefits, we need to combine
- triangle-based geometries and
- distances for them
... something like the distance maps, but 3D...
enter.... *drummroll*
SVO - Sparse Voxel Octrees
what?SVO - Sparse Voxel Octrees
Let's unroll it back-to-front:
-
Octree: 3D-equivalent of a 2D-Quadtree of a 1D-binary tree.
- base: cube, that can be split along 3 axis in 8 sub-cubes
-
Voxel: each node contains volumetric information:
- what's in that space, what's inside the cube?
- Sparse: the octree of voxels is sparsely populated. Easy :-).
SVO - Sparse Voxel Octrees
SVO - Sparse Voxel Octrees
SVOs:
- Huge Octree (GB's) on HD, load needed parts into memory
- Hybrid approach:
- Primary rays (cam): push geometry through rasterizer
- Following rays: Cone trace through SVO
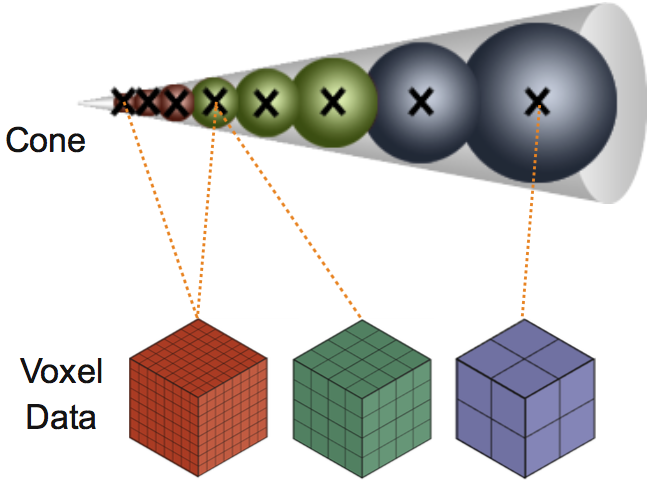
Voxel cone tracing:
- Start with bias size
- Progressively increase step size
- Lookup radiance & occlusion
- Accumulate light with occlusion
- Stop if occluded or too far
- Bonus: smooth occluders are further away $\rightarrow$ cheaper
SVO - Sparse Voxel Octrees
How do we use the SVO?
- Store distances in the octree
- Store material information
How do we store things in there?
How does the geometry come into play?
- Voxelize the scene into the octree!
- At runtime
... and no, I'm not kidding....
Unreal Engine 4

source: www.geforce.com
UE4 - Voxel Lighting
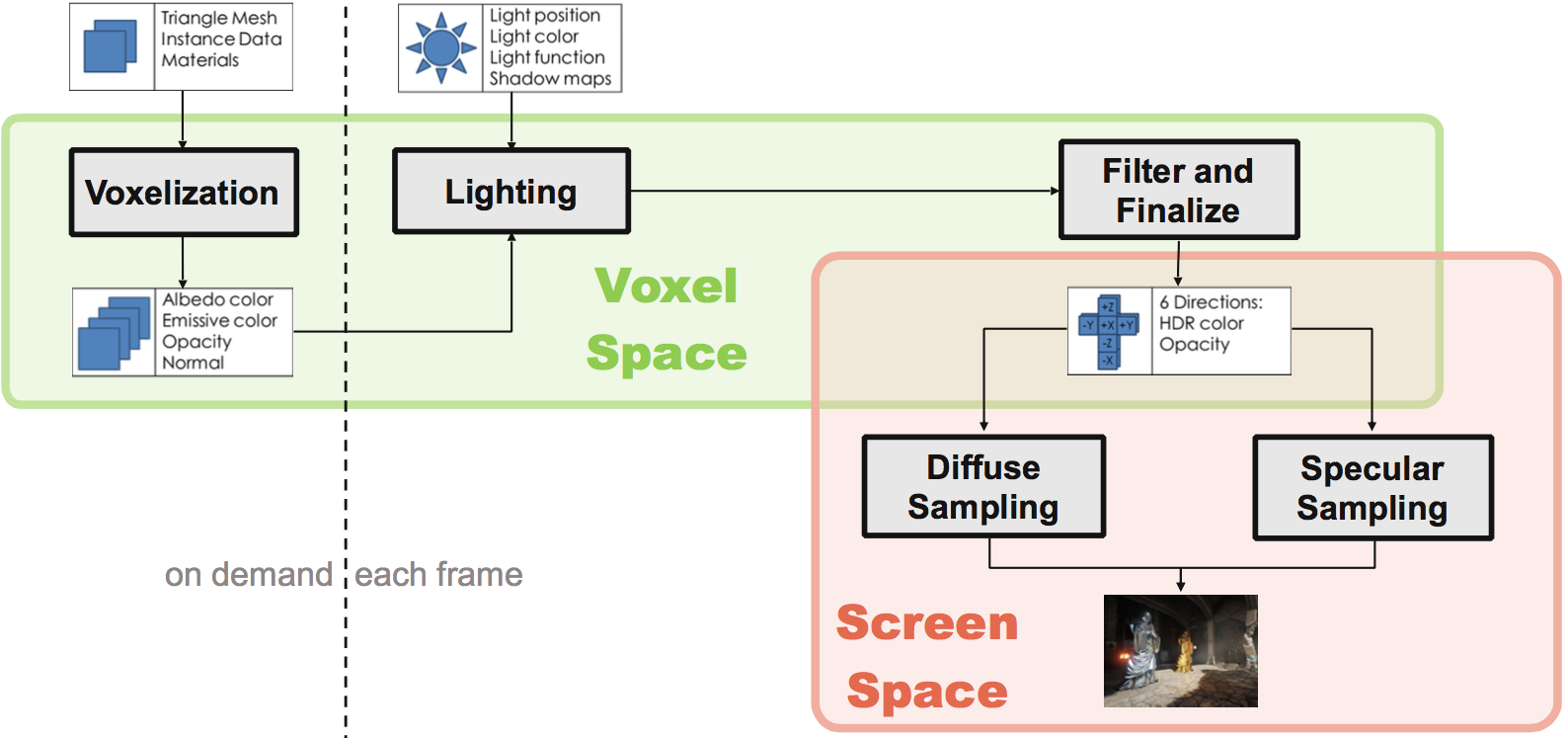
source: Epic Games
UE4 - Voxel Lighting
UE4 - Elemental Demo
Done.
Questions?
Selected References
- Alpha Tested Magnification
Chris Green - Valve - Antialiased 2D Grid, Marker, and Arrow Shaders
Nicolas P. Rougier - INRIA, CNRS, Bordeaux - Collected articles - read them all :-)
by Inigo Quilez - The Technology behind the Unreal Engine 4 Elemental Demo
Martin Mittrig - Epic Games